-
C = 1 Type = 1
Picture 1
C = 1 Type = 1
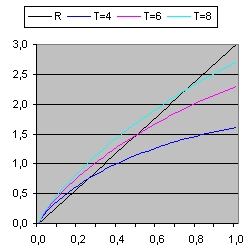
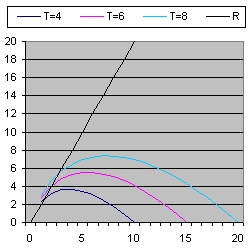
Picture 1 shows the evalution of three light signals when the expansion speed = c = 1.
The vertical axis shows de distance from the origon in one dimension in billion light years. The horizontal axis shows the time in Light years. The Big Bang is at the left.
Because the expansion speed is linear the radius R of the universe at any moment t is c*t = t.
This explains why the black line makes an angle of 45 degrees with the horizontal axis.
The light signals start at the rim of the universe when the universe is respectivily 4, 6 and 8 billion year old.
When the simulation starts the distance of the event is equal to the radius of the universe. That means when c=1 that the increase in distance caused by space expansion is equal as the distance of the light signal towards the observer. This explains why the initial direction of the light signal is horizontal.
Slowly the influence of the lightsignal increases compared to influence of space expansion. That is why the light signal bends.
At the end the influence of space expansion is zero. This explains why the final angle for each light signal is 45 degrees with the horizontal axis.
-
C = 2 Type = 1
Picture 2
C = 2 Type = 1
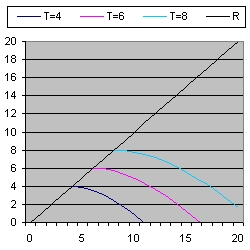
Picture 2 shows the evalution of three light signals when the expansion speed = c = 2.
The Black line shows the evolution of the radius R of the universe.
As a result when you compare Picture 2 with Picture 1 the Black line increases twice as fast.
The light signals start at the rim of the universe when the universe is respectivily 2, 3 and 4 billion year old and when the distance is respectivily 4, 6 and 8 billion lightyears.
When the simulation starts the distance of the event is equal to the radius of the universe. That means when c=2 that the increase in distance caused by space expansion is higher as the distance of the light signal towards the observer. This explains why the light signal first moves away from the observer.
In due time the increases caused by space expansion decreases until this increase becomes equal as the distance towards the observer.
This explains why the direction of the light signal becomes horizontal.
Slowly the influence of the lightsignal increases compared to influence of space expansion. That is why the light signal bends.
At the end the influence of space expansion is zero. This explains why the final angle for each light signal is 45 degrees with the horizontal axis.
-
C = 1 Type = 2
Picture 3
C = 1 Type = 2
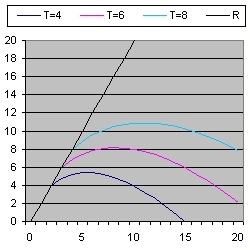
Picture 3 shows the evalution of three light signals when the expansion speed = c = 1. This is the same as Picture 1
The purpose of Picture 3 is to calculate the lightsignals when the Universe is respectivily 10, 15 and 20 billion years old. That means the start time of the events are unknown and because you want to calculate the oldest events which originated at the rim of the universe, this should be for each curve a point on the black line.
If possible this should be at the origin, which implies that you can observe the Big Bang.
In order to calculate this curve you need two initial events. Each of the events has a time and an initial distance. The time should be small (and at least before the initial event of the curve). In the program this is 50000 years.
For both events you calculate the final distance when the event reaches the observer.
- In one instance this final distance should be positive. This identifies initial distance high or disth
- In one instance this final distance should be negative. This identifies initial distance low or distl
Next you calculate a new initial distance which is equal to (disth+distl)/2
and you calculate the final distance when the event reaches the observer.
- When the final distance is positive you replace initial distance high or disth with this new initial distance
- When the final distance is negative you replace initial distance low or distl with this new initial distance
Next you calculate a new initial distance which is equal to (disth+distl)/2 and you repeat above for example 10 times.
-
C = 2 Type = 2
Picture 4
C = 2 Type = 2
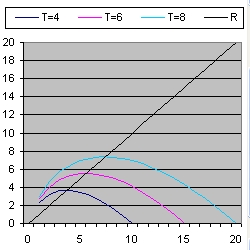
Picture 4 shows the evalution of three light signals when the expansion speed = c = 2.
When you compare Figure 4 with Figure 3 the difference is that the initial positions have changed. To be more specific when the expansion speed increases you will observe the same galaxies at an earlier instance.
However and that is important in none of these three cases you will be able to observe the Big Bang.
C = 1 Type = 1

Picture 1
C = 1 Type = 1
Picture 1 shows the evalution of three light signals when the expansion speed = c = 1.
The vertical axis shows de distance from the origon in one dimension in billion light years. The horizontal axis shows the time in Light years. The Big Bang is at the left.
Because the expansion speed is linear the radius R of the universe at any moment t is c*t = t.
This explains why the black line makes an angle of 45 degrees with the horizontal axis.
The light signals start at the rim of the universe when the universe is respectivily 4, 6 and 8 billion year old.
When the simulation starts the distance of the event is equal to the radius of the universe. That means when c=1 that the increase in distance caused by space expansion is equal as the distance of the light signal towards the observer. This explains why the initial direction of the light signal is horizontal.
Slowly the influence of the lightsignal increases compared to influence of space expansion. That is why the light signal bends.
At the end the influence of space expansion is zero. This explains why the final angle for each light signal is 45 degrees with the horizontal axis.
 |
Picture 1 shows the evalution of three light signals when the expansion speed = c = 1. The vertical axis shows de distance from the origon in one dimension in billion light years. The horizontal axis shows the time in Light years. The Big Bang is at the left. Because the expansion speed is linear the radius R of the universe at any moment t is c*t = t. This explains why the black line makes an angle of 45 degrees with the horizontal axis. The light signals start at the rim of the universe when the universe is respectivily 4, 6 and 8 billion year old. When the simulation starts the distance of the event is equal to the radius of the universe. That means when c=1 that the increase in distance caused by space expansion is equal as the distance of the light signal towards the observer. This explains why the initial direction of the light signal is horizontal. Slowly the influence of the lightsignal increases compared to influence of space expansion. That is why the light signal bends. At the end the influence of space expansion is zero. This explains why the final angle for each light signal is 45 degrees with the horizontal axis. |
C = 2 Type = 1

Picture 2
C = 2 Type = 1
Picture 2 shows the evalution of three light signals when the expansion speed = c = 2.
The Black line shows the evolution of the radius R of the universe.
As a result when you compare Picture 2 with Picture 1 the Black line increases twice as fast.
The light signals start at the rim of the universe when the universe is respectivily 2, 3 and 4 billion year old and when the distance is respectivily 4, 6 and 8 billion lightyears.
When the simulation starts the distance of the event is equal to the radius of the universe. That means when c=2 that the increase in distance caused by space expansion is higher as the distance of the light signal towards the observer. This explains why the light signal first moves away from the observer.
In due time the increases caused by space expansion decreases until this increase becomes equal as the distance towards the observer.
This explains why the direction of the light signal becomes horizontal.
Slowly the influence of the lightsignal increases compared to influence of space expansion. That is why the light signal bends.
At the end the influence of space expansion is zero. This explains why the final angle for each light signal is 45 degrees with the horizontal axis.
 |
Picture 2 shows the evalution of three light signals when the expansion speed = c = 2. The Black line shows the evolution of the radius R of the universe. As a result when you compare Picture 2 with Picture 1 the Black line increases twice as fast. The light signals start at the rim of the universe when the universe is respectivily 2, 3 and 4 billion year old and when the distance is respectivily 4, 6 and 8 billion lightyears. When the simulation starts the distance of the event is equal to the radius of the universe. That means when c=2 that the increase in distance caused by space expansion is higher as the distance of the light signal towards the observer. This explains why the light signal first moves away from the observer. In due time the increases caused by space expansion decreases until this increase becomes equal as the distance towards the observer. This explains why the direction of the light signal becomes horizontal. Slowly the influence of the lightsignal increases compared to influence of space expansion. That is why the light signal bends. At the end the influence of space expansion is zero. This explains why the final angle for each light signal is 45 degrees with the horizontal axis. |
C = 1 Type = 2

Picture 3
C = 1 Type = 2
Picture 3 shows the evalution of three light signals when the expansion speed = c = 1. This is the same as Picture 1
The purpose of Picture 3 is to calculate the lightsignals when the Universe is respectivily 10, 15 and 20 billion years old. That means the start time of the events are unknown and because you want to calculate the oldest events which originated at the rim of the universe, this should be for each curve a point on the black line.
If possible this should be at the origin, which implies that you can observe the Big Bang.
In order to calculate this curve you need two initial events. Each of the events has a time and an initial distance. The time should be small (and at least before the initial event of the curve). In the program this is 50000 years.
For both events you calculate the final distance when the event reaches the observer.
- In one instance this final distance should be positive. This identifies initial distance high or disth
- In one instance this final distance should be negative. This identifies initial distance low or distl
Next you calculate a new initial distance which is equal to (disth+distl)/2
and you calculate the final distance when the event reaches the observer.
- When the final distance is positive you replace initial distance high or disth with this new initial distance
- When the final distance is negative you replace initial distance low or distl with this new initial distance
Next you calculate a new initial distance which is equal to (disth+distl)/2 and you repeat above for example 10 times.
 |
Picture 3 shows the evalution of three light signals when the expansion speed = c = 1. This is the same as Picture 1 The purpose of Picture 3 is to calculate the lightsignals when the Universe is respectivily 10, 15 and 20 billion years old. That means the start time of the events are unknown and because you want to calculate the oldest events which originated at the rim of the universe, this should be for each curve a point on the black line. If possible this should be at the origin, which implies that you can observe the Big Bang. In order to calculate this curve you need two initial events. Each of the events has a time and an initial distance. The time should be small (and at least before the initial event of the curve). In the program this is 50000 years. For both events you calculate the final distance when the event reaches the observer.
and you calculate the final distance when the event reaches the observer.
|
C = 2 Type = 2

Picture 4
C = 2 Type = 2
Picture 4 shows the evalution of three light signals when the expansion speed = c = 2.
When you compare Figure 4 with Figure 3 the difference is that the initial positions have changed. To be more specific when the expansion speed increases you will observe the same galaxies at an earlier instance.
However and that is important in none of these three cases you will be able to observe the Big Bang.
 |
Picture 4 shows the evalution of three light signals when the expansion speed = c = 2. When you compare Figure 4 with Figure 3 the difference is that the initial positions have changed. To be more specific when the expansion speed increases you will observe the same galaxies at an earlier instance. However and that is important in none of these three cases you will be able to observe the Big Bang. |